Dr Pooya Sareh, Lecturer in Design Engineering, featured in Advances in Engineering
The least symmetric crystallographic derivative of the developable double corrugation surface
Computational design using underlying conic and cubic curves
Significance
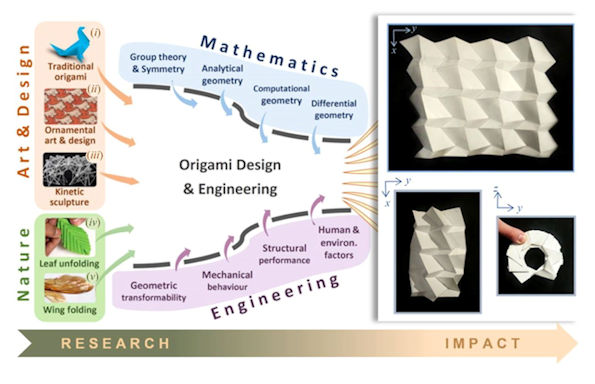
Origami is the art of paper folding – native to the Japanese culture – but its modern usage incorporates a broad range of folding theories, techniques, and practices. Over the years, origami design secrets have lured many mathematicians, engineers, and computer scientists, as this artistic approach has been proven to provide inspiration and innovative solutions to challenging scientific and engineering problems. So far, the flat-foldable origami tessellations have proved to be a rich source of inspiration, particularly in the design of transformable structures and mechanical metamaterials. Among all such tessellations, the developable double corrugation (DDC) surface, popularly known as the Miura-ori, is perhaps the most ubiquitous origami pattern in science, engineering, and architectural design. Origami artists, designers, and researchers in various fields of science and engineering have proposed a range of symmetric variations for this pattern. Noteworthy research has shown that designing many such derivatives is straightforward; however, some of them present considerable geometric or crystallographic challenges.
More often than not, the problem of finding flat-foldable derivatives for a given origami tessellation is more challenging for less symmetric descendants. Therefore, it is imperative that the existence and design of the least symmetric derivative of the DDC surface, i.e. the p1 derivative, with minimal unit cell enlargement, be studied. On this account, Dr. Pooya Sareh who is the Director of the Creative design engineering lab (Cdel) in the School of Engineering at the University of Liverpool in England probed the existence and design of the least symmetric derivative of the developable double corrugation surface with minimal unit cell enlargement in the longitudinal direction. His work is currently published in the research journal, Materials and Design.
In his approach, a typical two-by-two array of octagonal unit fragments associated with the derivative pattern was considered and possible solutions for flat-foldable vertices within the unit fragment explored. Dr. Pooya Sareh focused on delivering an approach adaptable and applicable to the design and development of possible non-trivial derivatives of other functional origami tessellations such as the Yoshimura fold pattern.
The author proved that the locus of points on a parallelogram-shaped flat sheet which are flat-foldable nodes when connected to its four vertices is of the hyperbolic family, which reduces to its diagonals when the parallelogram was a rhombus. In addition, he demonstrated that the corresponding locus for a general convex-quadrilateral is a cubic curve.
In summary, Dr. Pooya Sareh’ study demonstrated that a design challenge in the development of functional origami tessellations could be tackled using a combination of concepts and tools from origami, crystallography, and analytic and computational geometry. Furthermore, he showed that by reducing the intricate origami design problem to an analytic geometry problem, useful insights into more fundamental problems might be acquired. In a statement to Advances in Engineering, Dr. Pooya Sareh explained that the presented non-trivial solutions would enlarge the range of available preliminary concepts on which engineers and designers base the development of their applied research.
The article can be found in Advances in Engineering